Memahami Konsep Korelasi Pearson dalam Statistika
Memahami Konsep Korelasi Pearson dalam Statistika - Korelasi dalam penelitian didefinisikan sebagai hubungan antara dua variabel (atau lebih): yaitu variabel x dan variabel y. Uji Korelasi dalam Statistika menunjukkan “hubungan antara (minimal) dua variabel: variabel X (IV) dan variabel Y (DV)”
CONTOH:
Dalam statistika, hubungan antara x dan y dinyatakan dalam persamaan garis, yaitu garis regresi. Persamaan garis berguna apabila kita ingin membuat peramalan atau prediksi
y = f(x)
y = bx + a
Koefisien Korelasi
Ketika “hasil uji korelasi” dikuantifikasikan, maka nilai korelasi antara IV dan DV ditunjukkan dalam Koefisien Korelasi (r). Koefisien korelasi didefinisikan sebagai Angka yang menggambarkan bagaimana variasi pada satu variabel diikuti oleh variasi pada variabel yang lain. Koefisien korelasi dinyatakan dengan simbol: r; yang nilainya berkisar antara – 1 dan + 1
Nilai r = -1 atau +1 menunjukkan bahwa korelasi yang terjadi antara variabel X dan variabel Y adalah korelasi yang sempurna (kuat). Tanda negatif (-) dan positif (+) hanya menunjukkan arah hubungan antara variabel X dan Y.
Korelasi antara variabel memiliki dua arah:
Cohen (1988) mempublikasikan besaran korelasi menurut nilai koefisien korelasinya (r)
Jika r = 0, maka menunjukkan bahwa tidak ada korelasi yang terjadi antara variabel X dan variabel Y.
Ada beberapa keterbatasan yang menjadi karakteristik dari Uji Statistika Korelasi:
Dalam materi ini akan dijelaskan Korelasi Pearson product moment
Korelasi Pearson Product Moment diperkenalkan oleh Karl Pearson untuk melukiskan hubungan antara 2 buah variabel yang sama-sama berjenis interval atau sama-sama berjenis rasio. Untuk menghitung korelasi Pearson product moment dapat menggunakan rumus deviasi dan rumus angka kasar.
Ada persyaratan untuk melakukan analisa terhadap hasil Korelasi Pearson Product Moment, yaitu:
Rumus korelasi product moment:
CONTOH
Suatu penelitian dilakukan untuk melihat hubungan (korelasi) antara IV: Jumlah Absensi (absences) terhadap DV: Nilai Ujian (Exam Grade)
Tentukan Koefisien Korelasi (r) dan Buat Kesimpulannya!
Tahap 1: Tentukan H0 dan Ha/H1
“Tidak ada hubungan antara IV: jumlah absen (absences) terhadap DV: nilai ujian (exam grade)”
“Ada hubungan antara IV: jumlah absensi (absences) terhadap DV: nilai ujian (exam grade)”
Tahap 2: df, p, dan r table
Tahap 3: Tentukan koefisien korelasi (r)
SSX = 
SSY = 
SP =
Tahap 4: Buat Kesimpulan
atau
“Ada hubungan antara IV: jumlah absensi (absences) terhadap DV: nilai ujian (exam grade)
LATIHAN SOAL
Sekian artikel tentang Memahami Konsep Korelasi Pearson dalam Statistika. Semoga bermanfaat.
Daftar Pustaka
CONTOH:
- Hubungan antara “Motivasi Belajar” (IV) terhadap “Prestasi Belajar” (DV)
- Hubungan antara “Jumlah junkfood yang dikonsumsi perbulan” (IV) terhadap “jumlah lemak yang ditimbun”
Dalam statistika, hubungan antara x dan y dinyatakan dalam persamaan garis, yaitu garis regresi. Persamaan garis berguna apabila kita ingin membuat peramalan atau prediksi
y = f(x)
y = bx + a
 |
| image source: www.wikihow.com |
baca juga: Konsep Chi-Square Sebagai Alat Uji Hipotesa dalam Statistika
Koefisien Korelasi
Ketika “hasil uji korelasi” dikuantifikasikan, maka nilai korelasi antara IV dan DV ditunjukkan dalam Koefisien Korelasi (r). Koefisien korelasi didefinisikan sebagai Angka yang menggambarkan bagaimana variasi pada satu variabel diikuti oleh variasi pada variabel yang lain. Koefisien korelasi dinyatakan dengan simbol: r; yang nilainya berkisar antara – 1 dan + 1
Korelasi antara variabel memiliki dua arah:
- Korelasi Positif → korelasi yang ditunjukkan ketika salah satu variabel memiliki ‘nilai (skor)’ tinggi, maka variabel lainnya juga akan memiliki ‘nilai (skor)’ tinggi
- Korelasi negatif → korelasi yang ditunjukkan ketika salah satu variabel memiliki ‘nilai (skor)’ tinggi, maka variabel lainnya akan memiliki ‘nilai (skor) rendah”
 |
| (a) Korelasi Positif |
 |
| (b) Korelasi Negatif |
| Besaran Korelasi | Koefisien Korelasi (r) |
| Kecil | 0,1 – 0,3 |
| Sedang | 0,3 – 0,5 |
| Besar | > 0,5 |
- Uji Statistika Korelasi tidak menunjukkan hubungan sebab-akibat
- Variabel-variabel yang diuji memiliki kisaran data yang terbatas
- Data-data dengan nilai ekstrim mempengaruhi koefisien korelasi
Dalam materi ini akan dijelaskan Korelasi Pearson product moment
Korelasi Pearson Product Moment diperkenalkan oleh Karl Pearson untuk melukiskan hubungan antara 2 buah variabel yang sama-sama berjenis interval atau sama-sama berjenis rasio. Untuk menghitung korelasi Pearson product moment dapat menggunakan rumus deviasi dan rumus angka kasar.
Ada persyaratan untuk melakukan analisa terhadap hasil Korelasi Pearson Product Moment, yaitu:
- Jika rhitung (pearson) > r tabel (pearson), maka korelasi yang terjadi antara variabel X dan Y signifikan. Hasil perhitungan r menyebabkan H0 dapat ditolak; sehingga dapat dinyatakan ada hubungan signifikan antara dua variabel yang diteliti
- rhitung (pearson) < r tabel (pearson), maka korelasi yang terjadi antara variabel X dan Y tidak signifikan. Hasil perhitungan r menyebabkan H0 gagal ditolak; sehingga dapat dinyatakan tidak ada hubungan signifikan antara dua variabel yang diteliti
Rumus korelasi product moment:
Suatu penelitian dilakukan untuk melihat hubungan (korelasi) antara IV: Jumlah Absensi (absences) terhadap DV: Nilai Ujian (Exam Grade)
Tahap 1: Tentukan H0 dan Ha/H1
- H0: “Tidak ada perbedaan nilai ujian (exam grade) antara partisipan yang memiliki jumlah absen (absences) yang berbeda”
“Tidak ada hubungan antara IV: jumlah absen (absences) terhadap DV: nilai ujian (exam grade)”
- Ha/H1:“Ada perbedaan nilai ujian (exam grade) antara partisipan yang memiliki jumlah absen (absences) yang berbeda”
“Ada hubungan antara IV: jumlah absensi (absences) terhadap DV: nilai ujian (exam grade)”
Tahap 2: df, p, dan r table
- dfr = N – 2 = 10 – 2 = 8
- p < 0,05
- r tabel = 0,549
Tahap 3: Tentukan koefisien korelasi (r)


SP =

Tahap 4: Buat Kesimpulan
- r Hitung > r tabel → H0 ditolak, Ha/H1 diterima
atau
“Ada hubungan antara IV: jumlah absensi (absences) terhadap DV: nilai ujian (exam grade)
- r = – 0,85 → arah korelasi negatif → ketika jumlah absensi (absences) semakin besar, maka nilai ujian (exam grade) semakin kecil; ketika jumlah absensi (absences) semakin kecil, maka nilai ujian (exam grade) semakin besar
LATIHAN SOAL
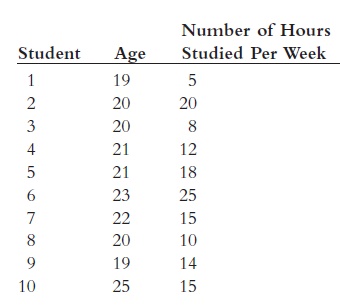
- Tentukan Koefisien Korelasinya dan Kesimpulannya dari data berikut ini
- Tentukan Koefisien Korelasinya dan Kesimpulannya dari data berikut ini
Daftar Pustaka
- Aron, A., Coups, E.J., & Aron, E.N. (2013). Statistics for psychology. 6th ed. New Jersey: Pearson Education, Inc.
- Gravetter, F.J. & Wallnau, L.B. (2009). Statistics for the Behavioral Sciences.
- Hinton, P.R. (2004). Statistics Explained, 2nd ed. London: Routledge.
- Howell, D.C. (2012). Statistical Method for Psychology. Australia: Wadsworth, Cengage Learning.
- Nolan, S.A. & Heinzen, T.E, (2012). Statistics for the Behavioral Sciences. Second Edition. New York: Worth Publishers.
- Sulistiyono, S. (2009). Statistika Psikologi 2. Jakarta: Fakultas Psikologi Universitas Mercu Buana.
Open Comments
Close Comments