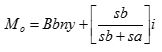Memahami Pengertian Tendensi Sentral dalam Statistika
Memahami Pengertian dan Ukuran Tendensi Sentral dalam Statistika - Artikel ini akan membahas tentang apa dan mengapa tendensi sentral, mean, median, modus, dan kapan suatu perhitungan tendensi sentral diperlukan. Melalui artikel ini diharapkan dapat memahami pengertian nilai sentral, dapat menentukan nilai-nilai sentral dari suatu distribusi, dan memahami penggunaan masing-masing nilai sentral.
Tendensi Sentral (Central Tendency)
Tendensi sentral adalah sering djadikan acuan memahami distribusi dari suatu data, dianggap sebagai sumber informasi penting yang menggambarkan distribusi suatu gejala atau fenomena. Di dalam modul ini akan dijelaskan apa yang dimaksud dengan tendensi sentral, fungsi dari tendensi sentral, cara menentukan suatu tendensi sentral, serta kapan suatu tendensi sentral digunakan
Distribusi Data
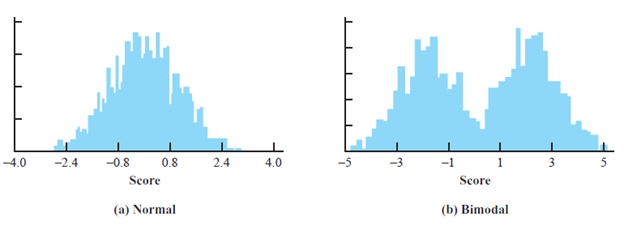
Dalam analisa statistika, dikenal berbagai jenis distribusi data. Beberapa contoh distribusi data ditampilkan di bawah ini.
Apa dan Mengapa Tendensi Sentral
Tendensi sentral memberikan satu nilai yang dapat mewakili/menggambarkan seluruh skor dalam kelompok, merupakan deskripsi ringkas dari sejumlah data kuantitatif yang didapat dari sampel dengan ekonomis, praktis, dan ringkas. Dengan tendensi sentral memungkinkan kita melakukan perbandingan antar kelompok; serta memungkinkan kita untuk melakukan proses statistik berikutnya seperti melihat hubungan (korelasi), perbedaan (t-test) antar kelompok, dan lain sebagainya.
Dari berbagai macam pengukuran tendensi sentral, ada 3 yang paling umum dikenal, yaitu: Mean (rata-rata), Median, dan Modes (modus). Ketiga jenis pengukuran tendensi sentral tersebut akan menjadi pokok pembahasan dalam modul ini.
Mean (Rata-rata)
Mean atau Rata-rata adalah pengukuran tendensi sentral yang paling sering digunakan. Hal ini berkaitan dengan nilai mean atau rata-rata yang relatif dianggap lebih mudah ditemukan dengan melakukan fungsi pembagian pada hasil penjumlahan nilai-nilai (score) yang ada pada data terhadap jumlah total frekuensi kemunculan nilai pada data tersebut. Untuk lebih mudah dipahami, nilai mean atau rata-rata dapat dicari dengan menggunakan rumus sebagai berikut:
Keterangan:
Pengukuran Mean atau Rata-rata pada data yang tidak berkelompok dapat langsung dilakukan dengan menggunakan rumus dasar perhitungan mean seperti yang tertera di atas:
Keterangan:
CONTOH:
Hitunglah mean atau rata-rata dari data tidak berkelompok: 1,2,3,4,5
Untuk data berkelompok sederhana (bukan data dengan skala interval), mean atau rata-rata dapat dicari dengan menggunakan rumus di bawah ini:
Keterangan:
CONTOH:
Tentukan mean atau rata-rata dari tabel distribusi frekuensi berikut ini:
Untuk data dengan skala interval, pengukuran mean atau rata-rata dapat dilakukan dengan menggunakan mean atau rata-rata terkaan. Rumus yang dapat digunakan yaitu:
CONTOH:
CONTOH:
Carilah mean dari sejumlah nilai mean di bawah ini:
Median
Median adalah Titik yang membagi suatu distribusi frekuensi atas dua bagian yang sama, yang masing-masing terdiri atas 50% kasus dari seluruh distribusi (Median = P50).
Di dalam data tidak berkelompok, yang nilai-nilainya sudah diurutkan berdasarkan besarannya, Median adalah nilai (score) ke-(N + 1)/2 dalam sederetan nilai yang berurutan.
CONTOH:
Nilai median dari data: 7, 7, 8, 9, 10, 11, 12 = 9
Nilai median dari data: 7, 7, 8, 9, 10, 11 = 8,5
Untuk data yang berkelompok, pengukuran Median dapat dilakukan dengan menggunakan rumus:
CONTOH:
Dari data berikut ini, carilah nilai mediannya:
Modes (Modus)
Modus adalah poin (titik nilai) pada skala pengukuran dengan frekuensi terbanyak pada suatu distribusi. Modus menunjukkan titik dalam suatu penyebaran yang paling padat/tinggi konsentrasinya. Ada beberapa teknik pengukuran Modus, di antaranya:
Mo = 3 Median – 2 Mean
M0 = Modus
Bbny = Batas bawah nyata dari kelas yang mengandung modus.
sb = Selisih frekuensi kelas yang mengandung M0 dengan frekuensi kelas dibawahnya.
sa = Selisih frekuensi kelas yang mengandung M0 dengan frekuensi kelas diatasnya.
i = Lebar interval.
CONTOH:
Dari data berkelompok berikut ini:
Tentukan Modus sebenarnya:
KAPAN PENGUKURAN MEAN, MEDIAN ATAU MODUS DIPERLUKAN?
Pengukuran Mean atau Rata-rata diperlukan untuk perhitungan statistik lebih lanjut; apabila data yang dianalisa memiliki penyebaran/distribusi frekuensi simetris dan tidak skewed; atau apabila diinginkan suatu tendensi sentral yang reliable.
Sementara, pengukuran Median diperlukan apabila ada nilai ekstrim dalam distribusi frekuensi yang mempengaruhi mean atau apabila titik tengah dari distribusi frekuensi ingin diketahui.
Pengukuran Modus diperlukan dalam analisa statistika jika diinginkan suatu ukuran pemusatan yang dapat dihitung dengan cepat atau apabila ingin diketahui skor yang khas.
SOAL LATIHAN
Tentukan Mean, Median dan Modusnya!
Tentukan:
Mean, Median, Modus Kasar dan Modus Sebenarnya!
Sekian artikel tentang Memahami Pengertian dan Ukuran Tendensi Sentral dalam Statistika. Semoga bermanfaat.
Daftar Pustaka
Tendensi Sentral (Central Tendency)
Tendensi sentral adalah sering djadikan acuan memahami distribusi dari suatu data, dianggap sebagai sumber informasi penting yang menggambarkan distribusi suatu gejala atau fenomena. Di dalam modul ini akan dijelaskan apa yang dimaksud dengan tendensi sentral, fungsi dari tendensi sentral, cara menentukan suatu tendensi sentral, serta kapan suatu tendensi sentral digunakan
baca juga: Memahami Penyajian Data Statistika dalam Tabel dan Grafik
Distribusi Data
Dalam analisa statistika, dikenal berbagai jenis distribusi data. Beberapa contoh distribusi data ditampilkan di bawah ini.
Gambar 1. Jenis-Jenis Distribusi Data
Apa dan Mengapa Tendensi Sentral
Tendensi sentral memberikan satu nilai yang dapat mewakili/menggambarkan seluruh skor dalam kelompok, merupakan deskripsi ringkas dari sejumlah data kuantitatif yang didapat dari sampel dengan ekonomis, praktis, dan ringkas. Dengan tendensi sentral memungkinkan kita melakukan perbandingan antar kelompok; serta memungkinkan kita untuk melakukan proses statistik berikutnya seperti melihat hubungan (korelasi), perbedaan (t-test) antar kelompok, dan lain sebagainya.
Dari berbagai macam pengukuran tendensi sentral, ada 3 yang paling umum dikenal, yaitu: Mean (rata-rata), Median, dan Modes (modus). Ketiga jenis pengukuran tendensi sentral tersebut akan menjadi pokok pembahasan dalam modul ini.
Mean (Rata-rata)
Mean atau Rata-rata adalah pengukuran tendensi sentral yang paling sering digunakan. Hal ini berkaitan dengan nilai mean atau rata-rata yang relatif dianggap lebih mudah ditemukan dengan melakukan fungsi pembagian pada hasil penjumlahan nilai-nilai (score) yang ada pada data terhadap jumlah total frekuensi kemunculan nilai pada data tersebut. Untuk lebih mudah dipahami, nilai mean atau rata-rata dapat dicari dengan menggunakan rumus sebagai berikut:
- Pengukuran Mean atau Rata-rata dari Data Tidak Terkelompok (Ungrouped data)
Pengukuran Mean atau Rata-rata pada data yang tidak berkelompok dapat langsung dilakukan dengan menggunakan rumus dasar perhitungan mean seperti yang tertera di atas:
CONTOH:
Hitunglah mean atau rata-rata dari data tidak berkelompok: 1,2,3,4,5
- Pengukuran Mean atau Rata-rata dari Data Berkelompok (Grouped data)
Untuk data berkelompok sederhana (bukan data dengan skala interval), mean atau rata-rata dapat dicari dengan menggunakan rumus di bawah ini:
CONTOH:
Tentukan mean atau rata-rata dari tabel distribusi frekuensi berikut ini:
| X | f | fX |
| 5 | 2 | 10 |
| 4 | 6 | 24 |
| 3 | 5 | 15 |
| 2 | 4 | 8 |
| 1 | 3 | 3 |
| Σ | 20 | 60 |
Untuk data dengan skala interval, pengukuran mean atau rata-rata dapat dilakukan dengan menggunakan mean atau rata-rata terkaan. Rumus yang dapat digunakan yaitu:
| X = Xs + (Σ fx’) i N |
| X = Rata-rata Xs = Rata-rata Terkaan (nilai tengah dari interval kelas yang diduga mengandung rata-rata. Σ fx’ = frekuensi dari durasi kesalahan terkaan (x’) i = Lebar interval kelas N = Jumlah frekuensi |
CONTOH:
| X | f | Mid Point | x’ | f . x’ |
| 177-179 | 1 | 178 | + 18 | 18 |
| 174-176 | 1 | 175 | + 15 | 15 |
| 171-173 | 5 | 172 | + 12 | 60 |
| 168-170 | 1 | 169 | + 9 | 9 |
| 165-167 | 10 | 166 | + 6 | 60 |
| 162-164 | 9 | 163 | + 3 | 27 |
| 159-161 | 16 | 160 | 0 | 0 |
| 156-158 | 11 | 157 | - 3 | - 33 |
| 153-155 | 13 | 154 | - 6 | - 78 |
| 150-152 | 7 | 151 | - 9 | - 63 |
| 147-149 | 3 | 148 | - 12 | - 36 |
| 144-146 | 1 | 145 | - 15 | - 15 |
| 78 |
| X = Xs + (Σfx’) i = 160 + (-36) 3 = 160 – 1,38 = 158, 62 N 78 |
- Pengukuran Mean atau Rata-rata dari sejumlah Nilai Rata-rata
| BRX = nilai rata-rata sejumlah nilai rata-rata SNi = jumlah frekuensi masing-masing kelompok data Xi = nilai rata-rata setiap kelompok |
CONTOH:
Carilah mean dari sejumlah nilai mean di bawah ini:
| Kelompok | Ni | Xi |
| A | 60 | 163 |
| B | 62 | 163 |
| C | 65 | 165 |
| BRX = (SNiXi) = ((60)(163)) + ((62)(163)) + ((65)(165)) = 9780 + 10.106 + 10.725 S Ni 60 + 62 + 65 187 = 30611 = 163,70 187 |
| BRX = (SNiXi) S Ni |
Median
Median adalah Titik yang membagi suatu distribusi frekuensi atas dua bagian yang sama, yang masing-masing terdiri atas 50% kasus dari seluruh distribusi (Median = P50).
- Data tidak terkelompok (Ungrouped Data)
Di dalam data tidak berkelompok, yang nilai-nilainya sudah diurutkan berdasarkan besarannya, Median adalah nilai (score) ke-(N + 1)/2 dalam sederetan nilai yang berurutan.
CONTOH:
Nilai median dari data: 7, 7, 8, 9, 10, 11, 12 = 9
Nilai median dari data: 7, 7, 8, 9, 10, 11 = 8,5
- Data berkelompok (Grouped Data)
Untuk data yang berkelompok, pengukuran Median dapat dilakukan dengan menggunakan rumus:
| Me = Median fkb = Frekuensi kumulatif dibawah frekuensi kumulatif yang mengandung Me f = Frekuensi dari kelas yang mengandung Me i = Lebar interval kelas yang mengandung Me |
CONTOH:
Dari data berikut ini, carilah nilai mediannya:
Modus adalah poin (titik nilai) pada skala pengukuran dengan frekuensi terbanyak pada suatu distribusi. Modus menunjukkan titik dalam suatu penyebaran yang paling padat/tinggi konsentrasinya. Ada beberapa teknik pengukuran Modus, di antaranya:
- Pengukuran Modus Kasar (crude mode)
- Data tidak berkelompok
- Data berkelompok
- Pengukuran Modus sebenarnya (true mode)
- Data tidak berkelompok
Mo = 3 Median – 2 Mean
- Data berkelompok
Bbny = Batas bawah nyata dari kelas yang mengandung modus.
sb = Selisih frekuensi kelas yang mengandung M0 dengan frekuensi kelas dibawahnya.
sa = Selisih frekuensi kelas yang mengandung M0 dengan frekuensi kelas diatasnya.
i = Lebar interval.
CONTOH:
Dari data berkelompok berikut ini:
| Nilai | F |
| 35 – 39 | 2 |
| 30 – 34 | 8 |
| 25 – 29 | 8 |
| 20 – 24 | 18 |
| 15 – 19 | 12 |
| 10 – 14 | 2 |
| Σ | 50 |
Tentukan Modus sebenarnya:
| 1. kelas yang mengandung M0 adalah 20 – 24 yang mempunyai f tertinggi yaitu 18). 2. Bbny = 19,5. 3. sa = 18 – 8 = 10 4. i = 5 5. sb = 18 – 12 = 6 6. = 21,375 |
KAPAN PENGUKURAN MEAN, MEDIAN ATAU MODUS DIPERLUKAN?
Pengukuran Mean atau Rata-rata diperlukan untuk perhitungan statistik lebih lanjut; apabila data yang dianalisa memiliki penyebaran/distribusi frekuensi simetris dan tidak skewed; atau apabila diinginkan suatu tendensi sentral yang reliable.
Sementara, pengukuran Median diperlukan apabila ada nilai ekstrim dalam distribusi frekuensi yang mempengaruhi mean atau apabila titik tengah dari distribusi frekuensi ingin diketahui.
Pengukuran Modus diperlukan dalam analisa statistika jika diinginkan suatu ukuran pemusatan yang dapat dihitung dengan cepat atau apabila ingin diketahui skor yang khas.
SOAL LATIHAN
- Berikut ini adalah tinggi badan10 mahasiswa Fakultas Psikologi
Tentukan Mean, Median dan Modusnya!
- 15 orang diminta untuk membawa buah-buah dadu dengan menggunakan kedua tangannya, sebanyak-banyaknya. Di bawah ini adalah catatan jumlah dadu maksimal yang dapat dibawa oleh partisipan penelitian dengan menggunakan kedua tangannya:
Mean, Median, Modus Kasar dan Modus Sebenarnya!
- Tentukan Mean, Median dan Modus (kasar dan sebenarnya) dari data berikut:
- Tentukan Mean, Median dan Modus dari data berikut ini:
Daftar Pustaka
- Howell, D.C. 2012. Statistical Method for Psychology.
- Gravetter, F.J. & Wallnau, L.B. 2009. Statistics for the Behavioral Sciences
- Nolan, S.A. & Heinzen, T.E, 2012. Statistics for the Behavioral Sciences. Second Edition.
Open Comments
Close Comments