Memahami Macam Ukuran Variabilitas dan Cara Menentukannya
Memahami Macam Ukuran Variabilitas dan Cara Menentukannya - Artikel ini akan membahas mengenai jangkauan total, jangkauan interkuartil, jangkauan semi interkuartil, mean deviasi, standard deviasi, varians, z-score, dan koefisien varians. Melalui artikel ini diharapkan dapat memahami berbagai macam ukuran variabilitas dan cara menentukannya.
Variabilitas
Dalam analisa statistika, informasi yang didapat melalui pengukuran tendensi sentral saja tidak cukup, karena tidak memberi informasi tentang sampel yang kita ukur secara menyeluruh. Tendensi sentral hanya memberikan informasi tentang suatu nilai yang menjadi pusat dari nilai-nilai lainnya, tetapi tidak memberikan informasi seberapa jauh atau seberapa besar nilai-nilai dalam kelompok itu bervariasi. Sebagai ilustrasi, coba perhatikan ketiga kelompok data berikut:
A : 25 25 25 25 25 25 25 25 25
B : 21 23 23 24 25 26 26 27 30
C : 6 15 15 21 25 27 30 41 45
Ketiga kelompok data di atas memiliki Mean atau Rata-rata yang sama, tetapi memiliki karakteristik data yang berbeda. Kelompok data A sangat homogen, sementara kelompok data B lebih homogen dibanding data C. Lalu, untuk mendapatkan informasi yang lebih jelas, pengukuran apa yang harus dilakukan?
Untuk memberikan gambaran ringkas yang memadai mengenai suatu distribusi data atau himpunan data, di samping dengan tendensi sentral juga diperlukan suatu ukuran variabilitas.
Variabilitas adalah derajat penyebaran nilai-nilai variabel dari tendensi sentralnya dalam suatu distribusi yang menunjukkan seberapa banyak nilai-nilai variabel itu berbeda dari tendensi sentralnya, atau seberapa jauh nilai-nilai varibel itu menyimpang dari tendensi sentralnya (terutama Mean atau Rata-rata). Pengukuran variabilitas akan memberikan gambaran variasi, jangkauan, serta heterogenitas-homogenitas dari pengukuran suatu kelompok (data).
BEBERAPA UKURAN VARIABILITAS
Sebagai contoh, perhatikan ketiga kelompok data berikut ini:
A : 25 25 25 25 25 25 25 25 25
B : 21 23 23 24 25 26 26 27 30
C : 6 15 15 21 25 27 30 41 45
Tentukan JT atau R!
JT atau R data A = 25 – 25 = 0
JT atau R data B = 30 – 21 = 9
JT atau R data C = 45 – 6 = 39
Pengukuran JT atau R relatif mudah dan cepat dihitung, tetapi tidak dapat diandalkan karena hanya berdasarkan nilai ekstrimnya saja. JT atau R mungkin memberikan gambaran yang salah tentang variabilitas, maka digunakan pengukuran Jangkauan semi interquartile (Q) yang memberikan informasi lebih baik dari JT atau R.
Berdasarkan ilustrasi di atas, pengukuran jangkauan semi interquartile (Q) dapat dijelaskan dengan menggunakan rumus berikut:
Q1 = kuartil pertama (P25)
Q2 = Median (P50)
Q3 = kuartil ketiga (P75)
Pengukuran MD untuk data tidak berkelompok dapat dilakukan dengan menggunakan rumus:
MD = Rata-rata simpangan
IxI = selisih X dari M ( dalam harga mutlak)
N = jumlah frekuensi
Sementara, untuk data berkelompok, pengukuran MD dapat dilakukan menggunakan tahapan berikut ini:
CONTOH:
SD = Ö [(å x2)/N]
Untuk pengukuran SD pada data berkelompok dalam tabel distribusi frekuensi, dapat dilakukan dengan menggunakan rumus:
SD = Ö [(å f(x2))/N]
Langkah-langkah penrhitungan SD dengan data berkelompok:
CONTOH:
Simpang baku dari beberapa distribusi yang digabungkan:
S1 & S2 = simpang baku dari distribusi 1 dan 2
d1 & d2 = X1 – X gabungan, X2 – X gabungan
N1 & N2 = jumlah individu dalam distribusi 1 dan 2
N = N1 + N2
KAPAN MENGGUNAKAN JT, Q DAN SD?
Pengukuran Jangkauan Total (JT) digunakan untuk menunjukkan variabilitas jika data yang ada terlalu sedikit atau terlalu terpencar; atau jika yang ingin diketahui hanya nilai (score) maksimum dan minimum dari distribusi.
Pengukuran Q digunakan jika median dipakai sebagai ukuran pemusatan; ada skor-skor yang terlalu ekstrim sehingga S akan memberikan gambaran yang menyesatkan; atau jika kasus-kasus di sekitar median dipentingkan.
Simpang baku (SD) digunakan bila diinginkan ukuran variabilitas yang paling stabil atau dapat diandalkan; bila diperlukan analisis statistik lebih lanjut; atau jika ingin membandingkan dua distribusi frekuensi.
VARIANS
Varians adalah kuadrat dari simpangan baku (SD2). Jadi kalau dari contoh pengukuran SD di atas, diperoleh SD = 1,285, maka variannya = SD2 = 1,2852 = 1,65. Namun, jika harga SD belum dihitung, maka varian dihitung dengan rumus sebagai berikut:
NILAI BAKU (Z SCORE)
Nilai baku adalah angka yang menunjukkan seberapa jauh suatu nilai (X) menyimpang dari rata-ratanya dalam satuan SD, merupakan indeks durasi suatu nilai. Nilai baku dapat dihitung dengan menggunakan rumus:
Z = Nilai baku
X = Suatu nilai (skor)
M = Rata - rata
SD = Simpangan baku
Perbedaannya dengan R dan SD, bahwa Z-score tidak lagi menggunakan angka kasar dan satuan pengukurannya, melainkan dalam satuan SD.
CONTOH:
Si A mendapatkan nilai matematika 50. Rata-rata kelompoknya adalah 40 dan SD = 5.
Maka nilai baku dari si A tersebut adalah :
KOEFISIEN VARIANS
Beberapa ukuran variabilitas yang telah dibahas di depan kesemuanya merupakan ukuran variasi absolut, hanya dapat untuk melihat penyimpangan nilai yang terdapat pada suatu himpunan data, dan tidak dapat digunakan untuk membandingkan beberapa himpunan data. Koefisien variasi (V) merupakan ukuran variasi yang bersifat relatif yang dapat digunakan untuk memperbandingkan beberapa himpunan data yang berbeda.
Koefisien varians dipakai jika hendak membandingkan S dari dua distribusi frekuensi yang tidak mempunyai satuan pengukuran yang sama; tidak mempunyai X yang sama; dan hanya boleh dipakai jika skala pengukuran adalah rasio
Koefisien Varians dapat dihitung menggunakan rumus:
V = Koefisien variasi
SD = Simpangan baku
M = Rata-rata
SOAL LATIHAN
Tentukan Q, MD, SD, Varians dan Koefisien Variasi dari data berikut ini:
18 15 22 19 18 17 18 20 17
12 16 16 17 21 23 18 20 21
20 20 15 18 17 19 20 23 22
10 17 19 19 21 20 18 18 24
11 19 31 16 17 15 19 20 18
Sekian artikel tentang Memahami Macam Ukuran Variabilitas dan Cara Menentukannya. Semoga bermanfaat.
Daftar Pustaka
Variabilitas
Dalam analisa statistika, informasi yang didapat melalui pengukuran tendensi sentral saja tidak cukup, karena tidak memberi informasi tentang sampel yang kita ukur secara menyeluruh. Tendensi sentral hanya memberikan informasi tentang suatu nilai yang menjadi pusat dari nilai-nilai lainnya, tetapi tidak memberikan informasi seberapa jauh atau seberapa besar nilai-nilai dalam kelompok itu bervariasi. Sebagai ilustrasi, coba perhatikan ketiga kelompok data berikut:
A : 25 25 25 25 25 25 25 25 25
B : 21 23 23 24 25 26 26 27 30
C : 6 15 15 21 25 27 30 41 45
Ketiga kelompok data di atas memiliki Mean atau Rata-rata yang sama, tetapi memiliki karakteristik data yang berbeda. Kelompok data A sangat homogen, sementara kelompok data B lebih homogen dibanding data C. Lalu, untuk mendapatkan informasi yang lebih jelas, pengukuran apa yang harus dilakukan?
 |
| image source: |
baca juga: Memahami Pengertian dan Ukuran Tendensi Sentral dalam Statistika
Untuk memberikan gambaran ringkas yang memadai mengenai suatu distribusi data atau himpunan data, di samping dengan tendensi sentral juga diperlukan suatu ukuran variabilitas.
Variabilitas adalah derajat penyebaran nilai-nilai variabel dari tendensi sentralnya dalam suatu distribusi yang menunjukkan seberapa banyak nilai-nilai variabel itu berbeda dari tendensi sentralnya, atau seberapa jauh nilai-nilai varibel itu menyimpang dari tendensi sentralnya (terutama Mean atau Rata-rata). Pengukuran variabilitas akan memberikan gambaran variasi, jangkauan, serta heterogenitas-homogenitas dari pengukuran suatu kelompok (data).
BEBERAPA UKURAN VARIABILITAS
- Jangkauan Total (total range) atau Rentangan Total (range of measurement)
JT atau R = skor maksimum – skor minimum
Sebagai contoh, perhatikan ketiga kelompok data berikut ini:
A : 25 25 25 25 25 25 25 25 25
B : 21 23 23 24 25 26 26 27 30
C : 6 15 15 21 25 27 30 41 45
Tentukan JT atau R!
JT atau R data A = 25 – 25 = 0
JT atau R data B = 30 – 21 = 9
JT atau R data C = 45 – 6 = 39
Pengukuran JT atau R relatif mudah dan cepat dihitung, tetapi tidak dapat diandalkan karena hanya berdasarkan nilai ekstrimnya saja. JT atau R mungkin memberikan gambaran yang salah tentang variabilitas, maka digunakan pengukuran Jangkauan semi interquartile (Q) yang memberikan informasi lebih baik dari JT atau R.
- Jangkauan semi interkuartil (Q)
Q = (Q3 – Q1)
2
Q1 = kuartil pertama (P25)
Q2 = Median (P50)
Q3 = kuartil ketiga (P75)
- Jangkauan antar kuartil
Jangkauan antar kuartil = Q3 – Q1
- Simpangan Rata-rata (Mean Deviation atau MD)
Pengukuran MD untuk data tidak berkelompok dapat dilakukan dengan menggunakan rumus:
MD = Rata-rata simpangan
IxI = selisih X dari M ( dalam harga mutlak)
N = jumlah frekuensi
- Hitung Mean
- Mengisi kolom x dengan cara X – Mean (dengan mengabaikan tanda negatif ).
- Mengisi kolom fx
- Menjumlahkan isi kolom fx (fx ≈ Σ ΙxΙ)
- Membagi jumlah isi kolom fx dengan n.
CONTOH:
- Simpang baku (standard deviation atau SD)
SD = Ö [(å x2)/N]
Untuk pengukuran SD pada data berkelompok dalam tabel distribusi frekuensi, dapat dilakukan dengan menggunakan rumus:
SD = Ö [(å f(x2))/N]
Langkah-langkah penrhitungan SD dengan data berkelompok:
- Hitung simpangan setiap skor dari nilai rata-ratanya : x = X - X
- Kuadratkan semua simpangan : x2
- Jumlahkan semua x2 : S x2
- Bagi jumlah ini dengan N : (S x2)/N atau (S (f(x2))/N
- Tarik akar : Ö[(S x2)/N] atau Ö[(S (f(x2))/N]
CONTOH:
| X | f | fX | x | fx | Fx2 |
| 9 | 2 | 18 | 2,5 | 5 | 12,50 |
| 8 | 7 | 56 | 1,5 | 10,5 | 15,75 |
| 7 | 12 | 84 | 0,5 | 6 | 3,00 |
| 6 | 10 | 60 | -0,5 | -5 | 2,50 |
| 5 | 6 | 30 | -1,5 | -9 | 13,50 |
| 4 | 3 | 12 | -2,5 | -7,5 | 18,75 |
| Σ | 40 | 260 | 43 | 66 |
- Simpangan Baku Gabungan
Simpang baku dari beberapa distribusi yang digabungkan:
Sgab = Ö [ N1 (S12 + d12) + N2 (S22 + d22)]/N
S1 & S2 = simpang baku dari distribusi 1 dan 2
d1 & d2 = X1 – X gabungan, X2 – X gabungan
N1 & N2 = jumlah individu dalam distribusi 1 dan 2
N = N1 + N2
KAPAN MENGGUNAKAN JT, Q DAN SD?
Pengukuran Jangkauan Total (JT) digunakan untuk menunjukkan variabilitas jika data yang ada terlalu sedikit atau terlalu terpencar; atau jika yang ingin diketahui hanya nilai (score) maksimum dan minimum dari distribusi.
Pengukuran Q digunakan jika median dipakai sebagai ukuran pemusatan; ada skor-skor yang terlalu ekstrim sehingga S akan memberikan gambaran yang menyesatkan; atau jika kasus-kasus di sekitar median dipentingkan.
Simpang baku (SD) digunakan bila diinginkan ukuran variabilitas yang paling stabil atau dapat diandalkan; bila diperlukan analisis statistik lebih lanjut; atau jika ingin membandingkan dua distribusi frekuensi.
VARIANS
Varians adalah kuadrat dari simpangan baku (SD2). Jadi kalau dari contoh pengukuran SD di atas, diperoleh SD = 1,285, maka variannya = SD2 = 1,2852 = 1,65. Namun, jika harga SD belum dihitung, maka varian dihitung dengan rumus sebagai berikut:
atau
Nilai baku adalah angka yang menunjukkan seberapa jauh suatu nilai (X) menyimpang dari rata-ratanya dalam satuan SD, merupakan indeks durasi suatu nilai. Nilai baku dapat dihitung dengan menggunakan rumus:
X = Suatu nilai (skor)
M = Rata - rata
SD = Simpangan baku
Perbedaannya dengan R dan SD, bahwa Z-score tidak lagi menggunakan angka kasar dan satuan pengukurannya, melainkan dalam satuan SD.
CONTOH:
Si A mendapatkan nilai matematika 50. Rata-rata kelompoknya adalah 40 dan SD = 5.
Maka nilai baku dari si A tersebut adalah :
Beberapa ukuran variabilitas yang telah dibahas di depan kesemuanya merupakan ukuran variasi absolut, hanya dapat untuk melihat penyimpangan nilai yang terdapat pada suatu himpunan data, dan tidak dapat digunakan untuk membandingkan beberapa himpunan data. Koefisien variasi (V) merupakan ukuran variasi yang bersifat relatif yang dapat digunakan untuk memperbandingkan beberapa himpunan data yang berbeda.
Koefisien varians dipakai jika hendak membandingkan S dari dua distribusi frekuensi yang tidak mempunyai satuan pengukuran yang sama; tidak mempunyai X yang sama; dan hanya boleh dipakai jika skala pengukuran adalah rasio
Koefisien Varians dapat dihitung menggunakan rumus:
SD = Simpangan baku
M = Rata-rata
Tentukan Q, MD, SD, Varians dan Koefisien Variasi dari data berikut ini:
18 15 22 19 18 17 18 20 17
12 16 16 17 21 23 18 20 21
20 20 15 18 17 19 20 23 22
10 17 19 19 21 20 18 18 24
11 19 31 16 17 15 19 20 18
Sekian artikel tentang Memahami Macam Ukuran Variabilitas dan Cara Menentukannya. Semoga bermanfaat.
Daftar Pustaka
- Howell, D.C. 2012. Statistical Method for Psychology.
- Gravetter, F.J. & Wallnau, L.B. 2009. Statistics for the Behavioral Sciences
- Nolan, S.A. & Heinzen, T.E, 2012. Statistics for the Behavioral Sciences. Second Edition.







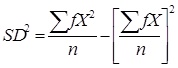


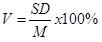

Posting Komentar untuk "Memahami Macam Ukuran Variabilitas dan Cara Menentukannya"